Mechanical-Electrical Analogies
Question
What is the equation governing the behaviour of a capacitor, that relates the current passing through it to the voltage across it?
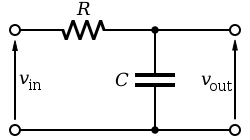
What is the purpose of the circuit below? The input $v_{\text{in} }$ is an AC wave, which takes a value $v_{\text{in} }=\sin(\omega t)$, where $\omega$ is the frequency of the input.
Electrical systems can be compared to mechanical systems. For this comparison, voltage (the 'effort variable') can be transformed to force, and current (the 'flow variable') can be transformed to velocity. What are the equivalent components for a mechanical system for a resistor and a capacitor?
What would be an equivalent mechanical circuit? Where would this be used?
Hints
For a capacitor, $ I = C \frac{dV}{dt} $
There are a few ways you can approach this question:
- find an expression for $v_{\text{out} }$
- consider the extreme cases where $\omega=0$ and $\omega$ is very large
- think about how the capacitor charges when the voltage steps from 0 to a constant. Then, think about the input switching on and off, alternating between discharging and charging. What happens when the rate of switching increases?
Answer
The voltage across $R$ is given by $IR$ (Ohm's law), as the current through the capacitor is equal to the current through the resistor.
If $\omega$ is small, then $I$ is small, and the voltage across the resistor, $v_{R}$, is small. This means that $$v_{\text{out} } = v_{\text{in} } - v_{R} \approx v_{\text{in} }$$
Conversely, for a large $\omega$, $I$ and $v_{R}$ are both large, and so the value of $v_{\text{out} }$ is small.
The circuit is therefore a lowpass filter. Signals at small frequencies are able to easily pass through, whereas large frequencies are reduced to zero. This can be useful in radios, for example, where only signals below a certain frequency are wanted, and high frequency noise is to be removed.
Resistors have the form $V=IR$, where the component resists flow of current. An equivalent
component is a damper, where $F=\lambda v$, where an force resists the velocity.
Capacitors behave as $ I = C \frac{dV}{dt} $. Transforming the variables to $ v = A \frac{dF}{dt} $.
Integrating both sides gives $ F = k x $, which is Hooke's law for a spring. Capacitors are
therefore equivalent to springs when transforming from electrical to mechanical systems.
An example of a mechanical lowpass filter is a suspension system in a car, which uses a spring.
For further reading, see this Wikipedia article
Also, have a look at this question about resistors and springs to further investigate how these systems can be compared.